EXERCISE 5.1
Question 1.Find the complement of each of the following angles: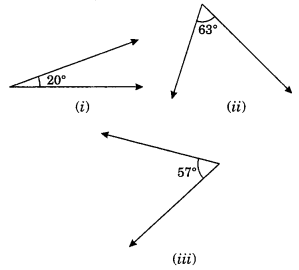
Solution:
(i) Complement of 20° = 90° – 20° = 70°
(ii) Complement of 63° = 90° – 63° = 27°
(iii) Complement of 57° = 90° – 57° = 33°
Question 2.Find the supplement of each of the following angles: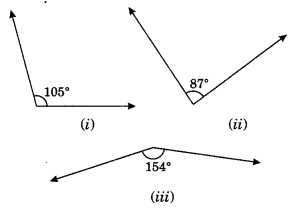
Solution:
(i) Supplement of 105° = 180° – 105° = 75°
(ii) Supplement of 87° = 180° – 87° = 93°
(iii) Supplement of 154° = 180° – 154° = 26°
Question 4.Find the angle which equal to its complement.
Solution:
Let the required angle be x°.
its complement = (90 – x)°
Now, re = 90 – x ⇒ x + x = 90
⇒ 2x = 90 ∴ x =
Thus the required angles are 45
Question 7.Can two angles be supplementary if both of them are:
(i) acute?
(ii) obtuse?
(iii) right?
(ii) Since, acute angle < 90°
∴ Acute angle + acute angle < 90° + 90° < 180° Thus, the two acute angles cannot be supplementary angles. (ii) Since, obtuse angle > 90°
∴ Obtuse angle + obtuse angle > 90° + 90° > 180°
Thus, the two obtuse angles cannot be supplementary angles.
(iii) Since, right angle = 90°
∴ right angle + right angle = 90° + 90° = 180°
Thus, two right angles are supplementary angles
Question 8. An angle is greater than 45°. Is its complementary angle greater than 45° or equal to 45° or less than 45 °?
Solution:
Given angle is greater than 45°
Let the given angle be x°.
∴ x > 45
Complement of x° = 90° – x° < 45° [ ∵ x > 45°]
Thus the required angle is less than 45
Question 10.Indicate which pairs of angles are:
(i) Vertically opposite angles
(ii) Linear pairs
Solution:
(i) Vertically opposite angles are ∠1 and ∠4, ∠5 and (∠2 + ∠3)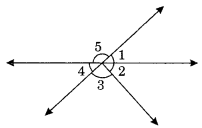
(ii) Linear pairs are
∠1 and ∠5, ∠5 and ∠4
Question 11.In the following figure, is ∠1 adjacent to ∠2? Give reasons.
Solution:
No, ∠1 and∠2 are not adjacent angles.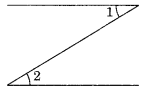
Reasons:
(i) ∠1 + ∠2 ≠ 180°
(ii) They have no common vertex
